|
||||||||||
|
|
||||||||||
|
||||||||||
|
|
||||||||||
|
|
|
||||||||||||
|
The first analytical theory to consider for a helicopter in forward (nonaxial) flight is the momentum theory. The
analysis for vertical (axial) flight is very similar to that of a simple propeller, and will not be discussed
here. One notable result of that analysis, however, is the induced velocity of the rotor in hover:
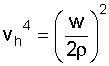
where w is the disc loading, given by
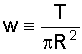
In the terms of basic momentum theory, the thrust of a rotor in nonaxial flight is very difficult to derive. In the context of this discussion, a relationship for the thrust that was proposed by Glauert in 1928 will be used. A simple diagram of an actuator disk in nonaxial flow is depicted below.
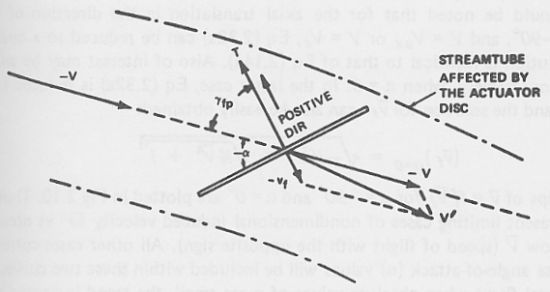
Actuator disk in nonaxial flow [from Stepniewski, 1979]The thrust of the actuator disk can be given by:
Far downstream from the disk, the downwash vf is doubled. Also, the term
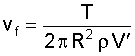
Unfortunately, this equation does not allow a determination of vf, since V´ is also dependent on vf. In order to solve for the induced velocity, V´ must first be expressed in terms of V and vf:
This value for V´ can then be substituted back into the thrust equation, which can then be nondimensionalized by vh (overbars denote nondimensional values):
The above equation can now be solved either graphically or with an iteration scheme. As a check of validity, if this equation is solved for an α of 0°, the solution matches that of the axial case. The other extreme case, where α=-90°, represents the other limiting case of helicopter forward flight. The nondimensional induced velocity versus the nondimensional flight velocity for both limiting cases are plotted below.
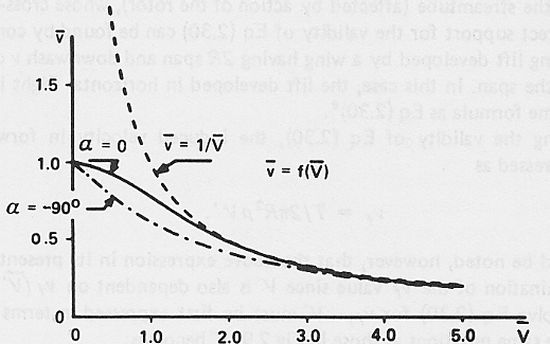
Nondimensional induced velocity versus nondimensional flight velocity [from Stepniewski, 1979]
While most cases of forward flight occur at small α, in which case the α=0° curve would be very
representative, all other intermediate cases of flight are within the two curves. It is important to note that
beyond a nondimensional flow velocity of about 3, the two curves are almost coincident, and can be approximated by
1/ |
|
Aircraft | Design | Ask Us | Shop | Search |
|
|
| About Us | Contact Us | Copyright © 1997- | |||
|
|
|||
becomes the mass flow through the stream tube that is
defined by the actuator disk. Some validity for these relationships can be inferred by comparing them to the
formula for the lift of a wing having 2R span with a uniform downwash. The lift of such a wing is expressed by an
equation similar to that shown above. After assuming that this equation is valid, determining the thrust requires
that the induced velocity in forward flight be determined:
.