Blade Element Theory in Forward Flight

Introduction Early History Modern History Flapping Hinges Maximum Speed Cyclic Control Momentum Theory Blade Element Theory Rotor Wake Summary References Home

Blade element theory provides the necessary means to predict the aerodynamic forces and moments acting on a rotor blade in forward flight. Similar to momentum theory, it is necessary to determine the magnitude and direction of the airflow in the immediate vicinity of the blade element under consideration. Once these velocities are known, the calculation of the forces and moments can be performed using two-dimensional airfoil characteristics, taking care not to neglect such aspects as Reynolds and Mach number effects. 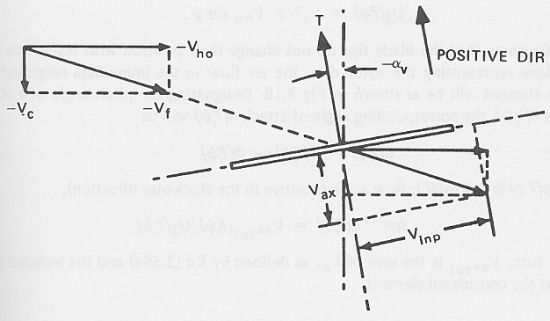Flow velocity components of a rotor in nonaxial flow [from Stepniewski, 1979] The flow velocity components of a rotor in nonaxial flow can be resolved into two components, the axial (Vax) and inplane (Vinp) components, both shown in the above figure. If a small tilt angle αv is assumed, then these components can be expressed as follows: As a first approximation, only the component of Vinp that is perpendicular to the blade axis is important (i.e. Vinp sin ψ. 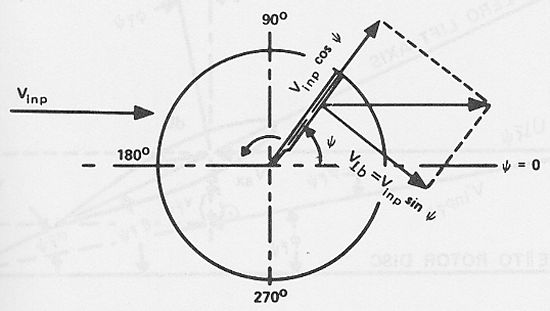Inplane velocity components [from Stepniewski, 1979] Also, in the case of forward flight when αv is small, the inplane velocity Vinp may be considered the same as the forward horizontal speed Vho. Taking into account the speed induced by the rotor rotation (ΩR) and the blade azimuth angle, the total component of the inplane velocity perpendicular to the blade axis is (overbars denote nondimensional values): If we assume that the blade tips maintain their position with respect to the TPP, then the flow velocities at a blade element are the same as those shown below. 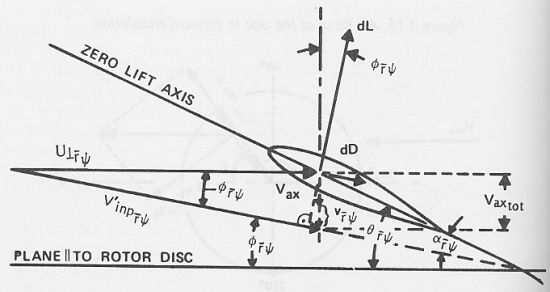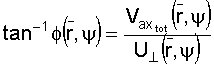Flow velocities at a blade element [from Stepniewski, 1979] The pitch angle of the blade is θ, the angle of attack, α, and the total inflow angle is φ, which gives the following equation: where Vax tot is the sum of Vax and the induced velocity v at the element. Assuming that the value of Vax tot is known, it is possible to calculate aerodynamic forces on a blade element. The three significant forces that can be calculated are thrust, dT, total drag, dD, and total torque, dQ. 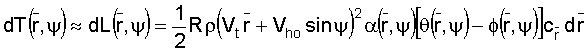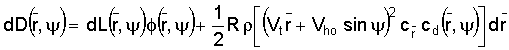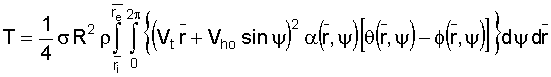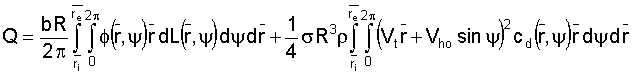For a rotor with rectangular blades, these equations can be integrated as follows: As with momentum theory, these equations can be integrated either graphically or numerically. Each integration yields the thrust or torque for a selected azimuth angle, which then must be averaged for a complete revolution of the blade. These values must then be multiplied by the number of blades to determine values for the entire rotor.

	Aircraft | Design | Ask Us | Shop | Search
	About Us | Contact Us | Copyright © 1997-2023