Aerospaceweb.org | Ask Us - Reference Area and Lift

Reference Area and Lift

_ref

- question from Scott Williams

The question you are referring to explains the terms used in the basic equation that describes how the lift of an airplane or helicopter is computed. Among these terms is the reference area, denoted by S_ref. Now the important thing to realize about reference area is that it is really only an arbitrary value. It exists because aeronautical engineers need some area by which to nondimensionalize the lift coefficient, as well as other aerodynamic coefficients (such as drag).

This is particularly true when it comes to collecting wind tunnel data. In the wind tunnel, balances are used to measure the actual lift or drag force as well as aerodynamic moments that are generated by some body in a given set of conditions (such as velocity and angle of attack). Knowing the forces and moments themselves is useful, but it is more convenient to express these values in terms of some nondimesional form that can be more easily compared for different configurations at different conditions.

Let us consider an example and compare the lift produced by a jet fighter to that produced by a sailplane. If you were to compare them simply of the amount of lift force they produce, the fighter would appear to be several orders of magnitude "better" at producing lift. But this is an unfair comparison simply because the fighter weighs orders of magnitude more than the sailplane and needs to generate that much more lift to remain airborne. But when we nondimensionalize the lift force and compare the two vehicles based on their lift coefficients, we'd see that in actuality the sailplane generates a higher lift coefficient making it the more effective lifting surface.

These nondimensional forms of the aerodynamic coefficient are expressed as C_L for lift, C_D for drag, C_m for pitching moment, and so on. So at this point, what we need is some way to convert the dimensional forces and moments expressed in pounds, Newtons, ounces, foot-pounds, Newton-meters, ounce-inches, or some other unit system into the nondimensional coefficient form. We can understand how this is done by turning back to our good old friend the lift equation:

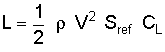
Here we see the dimensional form of lift (L, in pounds or Newtons) is computed as a function of operating conditions (density and velocity), reference area, and the lift coefficient. But in our case, we have specified the operating conditions in the wind tunnel and measured the lift force, so we can compute the lift coefficient in this way:

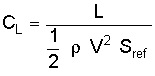
Here it is that we see how the term S_ref is needed simply as an area term to nondimensionalize the coefficient. And it really makes no difference what value we use so long as that same value is used consistently in any future work with that coefficient data. It is simply a rule of thumb that the wing area is used as the reference area for aircraft and the rotor area is used for helicopters. For rockets or missiles, we typically use the maximum cross-sectional area of the body. However, this is not always the case as for some missile configurations it makes more sense to use a wing or fin area or even a total planform area. For airfoils, we need a reference length rather than an area, so we use the chord, or length, of the airfoil section.

The key point to remember from this discussion is that the reference area itself has nothing to do with how much lift a vehicle produces, but it is important to know what area was used in a given application to make correct conclusions about the aerodynamic behavior of that body. If one were to conduct two wind tunnel tests of the same missile and in one case used the fin area as the reference area and in the other used the body cross-sectional area, one set of lift coefficients would likely appear to be much greater than the other, so a comparison of the two sets of data would be useless. Therefore, while it is not necessary to use wing area for planes, rotor area for helicopters, or cross-sectional area for missiles, it is useful to do so because it provides a common ground for comparison between the lift coefficient produced by two different planes, two different helicopters, or two different missiles.

As for number of blades and the blade airfoil section, of course these variables factor in to how much lift a helicopter rotor will generate. But the same can be said of an airplane where the wing airfoil section, the use of flaps or slats, wing incidence angle, and a variety of other factors will increase or decrease the amount of lift the plane generates. While these more complex considerations are not addressed directly in the basic equation for lift, where they do factor in is in the lift coefficient itself. For example, C_L increases with increasing angle of attack for both an aircraft wing and a helicopter rotor. The latter is accomplished by increasing the angle at which an individual rotor blade or all of the rotor blades collectively meets the oncoming air. Similarly, the increase in lift associated with a plane dropping flaps or slats is reflected in the lift equation through an increase in C_L. Keep in mind that this equation for lift is only a very basic expression used to analyze the overall aerodynamic behavior of an entire vehicle. Engineers must use much more complex methods to do detailed design and analysis work.
- answer by Jeff Scott, 19 May 2002

Is there a way to estimate the drag coefficient using Thin Airfoil Theory? I know that lift coefficient is estimated as 2*pi*alpha, but does Thin Airfoil Theory even predict a value for the drag coefficient?

I found equations for lift and drag for a 2D airfoil as a function of normal force, axial force, and angle of attack. ... I assumed some values, but the results seem totally wrong. ... Have I made a glaring omission or is there a physical explanation for this behavior?

Aircraft | Design | Ask Us | Shop | Search