Atmospheric Pressure

NOTE: The following explanation refers to the methods used in a previous version of the Atmospheric Properties Calculator. A revision explaining the more fundamental and accurate methods used in the current calculator will be provided as soon as possible. In any event, the equations described below still produce a close approximation of the standard atmosphere.

If I understand your question correctly, you want to know how to calculate the atmospheric pressure in pounds per square inch given the altitude. Below is a discussion of how the Atmospheric Properties Calculator works that I hope meets your needs. The following equations are based on material you should be able to find in any good basic aerodynamics textbook in a chapter covering atmospheric properties. All units are English, but the methodolgy can easily be adapted for use in the Metric system.

  1. provide the altitude (h) in feet

  2. set the sea level pressure (lb/ft²), a known constant
    PresSL = 2116.224

  3. set the default pressure ratio (Delta), or the "relative pressure" which is the ratio of the pressure at h over the pressure at sea level
    Delta = 1.0

  4. compute the new pressure ratio based on where you are in the atmosphere

      below 36,089 ft
      Delta = (1 - h/145442)^(5.255876)

      between 36,089 ft and 65,617 ft
      Delta = 0.223361 * exp( (36089-h)/20806 )

      between 65,617 ft and 104,987 ft
      Delta = (0.988626 + h/652600)^(-34.16319)

      between 104,987 ft and 154,199 ft
      Delta = (0.898309 + h/181373)^(-12.20114)

      between 154,199 ft and 167,323 ft
      Delta = 0.00109456 * exp( (h - 154200)/-25992 )

      between 167,323 ft and 232,940 ft
      Delta = (0.838263 - h/577922)^(12.20114)

  5. compute the pressure at h
    pressure = PresSL * Delta

  6. the above answer is in pounds per square foot (psf), convert the solution to different units if desired

    convert into multiply by
    psf psi 1 / 144
    psf atm 1 / 2116.224
    psf kPa 0.0478927
The same approach can also be used to compute other basic atmospheric properties, including temperature and density. Relationships between these most basic quantities can then used to derive other properties such as the speed of sound, viscosity, and kinematic viscosity. For the sake of completeness, we will include these calculations as well.
  1. provide the altitude (h) in feet

  2. set the sea level temperature (degrees Rankine) and density (slugs/ft³), known constants
    TempSL = 518.67
    RhoSL = 0.00237689

  3. set the default temperature ratio (Theta) and density ratio (Sigma), the ratios of the temperature or density at h over that at sea level
    Theta = 1.0
    Sigma = 1.0

  4. compute the new temperature and density ratios based on where you are in the atmosphere

      below 36,089 ft
      Theta = 1.0 - h/145442
      Sigma = (1.0 - h/145442)^(4.255876)

      between 36,089 ft and 65,617 ft
      Theta = 0.751865
      Sigma = 0.297076 * exp( (36089 - h)/20806 )

      between 65,617 ft and 104,987 ft
      Theta = 0.682457 + h/945374
      Sigma = (0.978261 + h/659515)^(-35.16319)

      between 104,987 ft and 154,199 ft
      Theta = 0.482561 + h/337634
      Sigma = (0.857003 + h/190115)^(-13.20114)

      between 154,199 ft and 167,323 ft
      Theta = 0.939268
      Sigma = 0.00116533 * exp( (h - 154200)/-25992 )

      between 167,323 ft and 232,940 ft
      Theta = 1.434843 - h/337634
      Sigma = (0.79899 - h/606330)^(11.20114)

  5. compute the temperature and density at h
    temperature = TempSL * Theta
    density = RhoSL * Sigma

  6. the temperature is in degrees Rankine and the density in slugs per cubic foot, some common conversions are provided below

    convert into conversion
    Rankine Fahrenheit subtract 460
    Rankine Kelvin divide by 1.8
    Kelvin Celsius subtract 273

    convert into multiply by
    sl/ft³ lbm/ft³ 32.174
    sl/ft³ kg/m³ 536.523

  7. compute the speed of sound, viscosity, and kinematic viscosity
    vel_sound = sqrt( 2403.184 * temperature ) [ft/sec]
    viscosity = 0.0226968 * (temperature^1.5) / (temperature + 198.72) / 1000000 [sl/ft/sec]
    kin_viscosity = viscosity / density [ft²/sec]

    convert into multiply by
    ft/sec mph 0.6818
    ft/sec m/sec 0.3048
    ft/sec km/h 1.097
    ft/sec knots 0.5921
    sl/ft/sec kg/m/sec 47.88
    ft²/sec m²/sec 0.0929

Using these relationships, you should obtain a reasonably accurate model of the actual standard atmosphere that is consistent with the results displayed in the following graph.

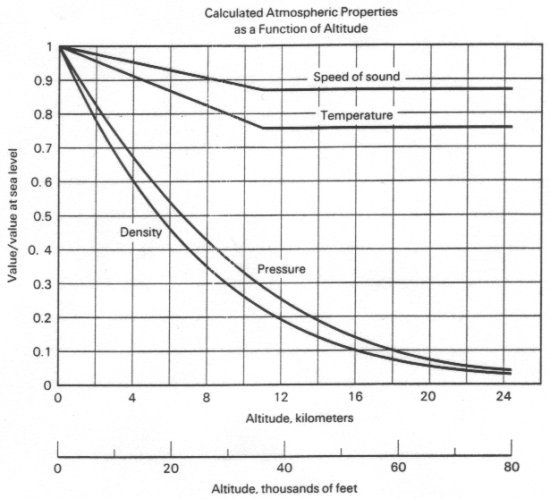
Changes in atmospheric properties with altitude
Changes in atmospheric properties with altitude

Also, the aforementioned Atmospheric Properties Calculator uses these equations to compute the above quantities automatically given nothing more than the altitude in English or Metric units. The calculator can also be used to find a number of other properties when provided with a velocity and a reference length of the body under study.
- answer by Jeff Scott, 21 October 2001

Related Topics:

Read More Articles:









Back Aircraft | Design | Ask Us | Shop | Search Home
About Us | Contact Us | Copyright © 1997-2023