|
||||||||||
|
|
||||||||||
|
||||||||||
|
|
||||||||||
T(X)=10*TC[0.2969(X/C)^0.5-0.126(X/C)-0.3537(X/C)^2+0.2843(X/C)^3-0.1015(X/C)^4]
In addition, how were the parabolic equations used to calculate the mean camber line derived? Why do they
have boundary conditions at x=0, x=p, and x=c?
- question from Yasser

Those preliminaries aside, let's get down to the heart of your question--where do these equations come from? I think you have a false impression that these relationships were somehow derived from some fundamental concepts of mathematics and physics, but this is not the case. The thickness equation, for example, is actually based on empirical studies conducted by NACA back in the 1930s. Until that time, airfoil design was really little more than magic. Early aircraft designers had experimented with a number of diferent shapes and just happened to stumble across a few that worked very well. No one really understood why some shapes worked and others didn't, so there was no theory to guide designers in selecting the best airfoils for a given application. Picking the right shape was a matter of luck.
Researchers at NACA were very curious about this subject, and one of the first major efforts undertaken by the organization after its founding was to bring some logic and reason to airfoil design. They started by trying to understand why some airfoils worked well and others did not. In the process, they realized that there were a lot of common features shared by the airfoils that were most successful. These features could be reproduced by a simple combination of a mean camber line and a thickness distribution. As illustrated below, the mean camber line (or simply "mean line") is a line running along the center of the airfoil. It can be thought of as the average of the upper surface and lower surface of the airfoil shape. The thickness distribution defines how thick the airfoil is at any point along its length above and below that mean line.
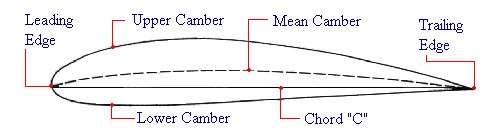
Armed with this knowledge, the researchers defined some simple algebraic equations that could be used to generate a family of airfoils similar to the successful shapes from which the equations were derived. The equations they came up with are empirical relationships. In other words, they happen to mathematically produce shapes similar to existing airfoils, but there is no fundamental theory underlying their development. They are merely equations that happened to fit the existing airfoil coordinate data. The mean camber line equations, in particular, were simply chosen to be parabolic equations arbitrarily since an equation of that form just happened to match the camber lines used on many of the successful airfoils of the day. By changing the value of p and its x-position along the chord, parabolic equations matched up well with the camber lines for these existing shapes.
Since you asked about sources describing how these equations were developed, you can read more in two classic publications:
Related Topics:
Read More Articles:


|
Aircraft | Design | Ask Us | Shop | Search |

|
|
| About Us | Contact Us | Copyright © 1997- | |||
|
|
|||