Airfoil Design

In the early days of aviation, airfoil design was in its infancy and designers depended on crude rules of thumb to develop the shapes used on their aircraft. Before long, a few very successful shapes were found and applied to many airplanes by a wide variety of manufacturers even though they had little idea of why they worked so well. By the early 1930s, the National Advisory Committee for Aeronautics (NACA) in the US began an effort to more systematically design and test new airfoils. These new airfoils shapes were developed mostly from geometric equations. In all these cases, the airfoils were tested in wind tunnels to determine their lift and drag performance at different angles of attack and airspeeds.

Today's airfoil designer has far more analytical tools at his disposal, although there are only two basic approaches to designing "experimental" airfoils. The first, the direct method, is essentially the same approach used by the early aviation pioneers. The design process consists of selecting a known airfoil shape with performance similar to that required by the new application and making slight modifications to the shape to achieve the required performance. A newer approach, made practical by the computer revolution, is known as the inverse method. Here, the designer specifies the performance characteristics required by the airfoil and uses computer programs to compute the airfoil geometry that produces that performance.

The advantage of the direct approach is its simplicity, although the time and cost required to build and test a significant number of modified airfoil shapes is prohibitive. In addition, there is no guarantee that these new shapes will achieve the performance levels originally specified. Thus, the inverse approach is far more powerful since the designer has much more precise control over the final performance of the airfoil and he can test a much greater number of shapes via computer than would be practical to build and test in the wind tunnel. However, while every airfoil shape produces a particular set of performance characteristics, not every set of performance characteristics can be used to generate a realistic airfoil shape. The designer must be aware of what is practical, the trade-offs required between different types of performance, and physical contraints (such as providing enough room for internal structure). Even once a promising shape has been found using computational methods, we must still test them using higher-level computer software, namely computational fluid dynamics (CFD) codes, or preferably in the wind tunnel. Confirmation using these additional methods gives the designer greater confidence that the airfoil will meet the required levels of performance.

The particulars of the mathematics used within these computer programs to compute the lift and drag of airfoils are not that difficult (to someone who has a degree in aerospace engineering!), but are probably a bit more complex than the average visitor to this site would care to read about. Some important methods include Thin Airfoil Theory, the Kutta-Joukowski Theorem, Panel Methods, the Integral Boundary Layer Method, and Conformal Mapping. If those names don't scare you off, then feel free to check out a good intermediate or advanced aerodynamics text book to learn more. What is useful to know is that these mathematical methods are already built into a number of airfoil design and analysis codes that are available on the web:

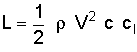
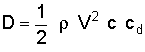
The above codes give the designer the lift coefficient (c l) and drag coefficient (c d) of the airfoil at various operating conditions (i.e. angles of attack, speeds, and altitudes). These coefficients are non-dimensional allowing the designer to quickly and easily compare values for different shapes at different conditions to find the optimum airfoil for the application. The actual lift and drag forces acting on the airfoil can then be computed using the equations

For an explanation of the terms in these equations, see a previous question on the lift equation. Note that the above equations are applicable to an airfoil only while the previous discussion related to a wing or an entire aircraft. Thus, the wing reference area S ref is now replaced by the length of the airfoil, called the chord and represented by c. In addition, we represent the two-dimensional lift of an airfoil by lowercase c l to distinguish it from the three dimensional lift of a wing or complete airplane represented by uppercase C L.
- answer by Jeff Scott, 15 July 2001

Read More Articles:









Back Aircraft | Design | Ask Us | Shop | Search Home
About Us | Contact Us | Copyright © 1997-2023